In queste pagine non ho la pretesa di esporre la teoria del sistema D’Appolito – per una trattazione completa dell’argomento rimando all’articolo AES del 1983[1] – l’obiettivo è esclusivamente di fornire qualche breve cenno in modo da rendere comprensibile il perché di alcune scelte progettuali.
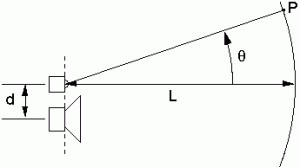
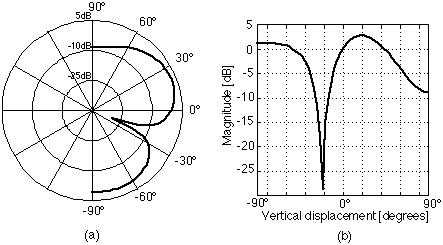
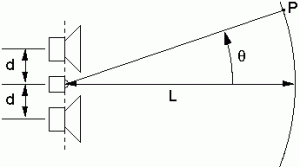
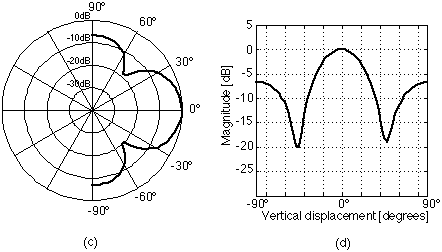
La configurazione MTM (Midwoofer Tweeter Midwoofer) venne proposta da Joseph D’Appolito come un approccio geometrico per eliminare la formazione di lobi nella risposta polare verticale di un diffusore a due vie tipico TM (Tweeter Midwoofer).
Confrontiamo entrambe le configurazione per chiarirci le idee prendendo in esame come esempio un filtro Butterworth del terzo ordine. Le immagine seguenti sono estratte dall’articolo Vertically Symmetric Two-Way Loudspeaker Arrays Reconsidered di Mithat F. Konar – Biro Tecnology[2].
Nel suo articolo D’Appolito ha mostrato matematicamente come calcolare la formazione dei lobi e ha confrontato i risultati ottenuti con un sistema MTM e diverse tipologie di filtro crossover. Dal suo studio si evince che i migliori risultati si ottengono con filtri Butterworth di ordine dispari, in particolare, con una Fc (frequenza di crossover) strettamente legata alla distanza d.
Il crossover passivo sarà, quindi, del terzo ordine acustico Butterworth, con Fc calcolata considerando la distanza “d” tra il centro del woofer e il centro del tweeter secondo la relazione:
d = 2/3 λc
(λc è la lunghezza d’onda della frequenza di crossover)
Nel nostro caso d è pari a 13,25 cm, trattandosi della distanza minima ottenibile montando gli altoparlanti il più vicino possibile.
Ma non si doveva calcolare d dipendentemente dalla Fc scelta?
Invece, ho fatto l’esatto contrario: ho fissato d e ho calcolato la Fc!
Data d = 13,25 cm = 0,1325 m, usando la formula inversa, si ottiene
λc = 3/2 d = 0,19875 m
da cui segue che la frequenza di taglio dovrà essere
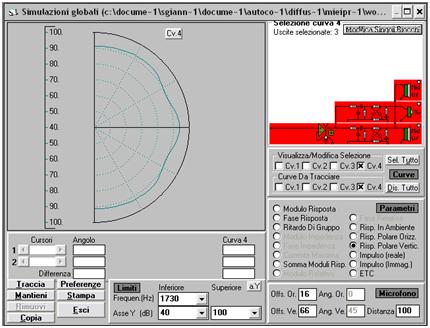
Fc = v/ λc = 1.730 Hz
[1] A geometrical approach to eliminating lobing error in multiway loudspeakers – Joseph D’Appolito – presented at the 74th AES Convention 1983 October 8-12 New York